解决的是一个类似于管道输送的问题。
假设现在有一个管道网络,一共有 $n$ 个节点,其中 $1$ 号点是源头,能源源不断地提供输送物;$n$ 号是接收点,接收所有到达的输送物;中间的节点是中转点,可以将受到的输送物送入其他的管道;管道有容量。求出能到达 $n$ 的最多输送物量。
求解网络最大流比较常用的算法是 Dinic,此外网络流常常利用建模思想来解决一些看似不好入手的题。看似不是图论的题
最大流算法
梦开始的地方:Ford-Fulkerson
FF 算法是增广路网络流算法的起源。
什么是增广路
简单来说,就是还能流的路径。
具体的,我们为一个网络建立残量网络,原图中的边保持不变,而对于每条边都有一个对应的反向边,初始容量为 $0$。
在 FF 算法中,每轮增广时会从 $s$ 开始 dfs,找出一条路径上流量非负为 $f$ 的路径,并且将沿着这条路径的边流量减少 $f$,并且将对应反向边流量增加 $f$。
不难发现反向边的作用在于给算法一个反悔的机会:流过去之后还可以“反悔”,再流回来,这两种过程是等效的,但是避免了算法每一步都要最优化。
不难发现一次增广至少会流 $1$,时间复杂度是 $O(n\times\text{maxflow})$。
当边权巨大的时候就寄了,所以需要一个不依赖于边权的算法。
EK 算法:多项式算法
上面的 FF 算法中可能会陷入一个反悔的困境,导致其时间复杂度非常大。因此 EK 算法利用 bfs 代替 dfs,来寻找可行的增广路。
EK 算法在当前残量网络上利用 bfs 来为节点按照深度编号并且找到最短的增广路。然后再利用这条增广路来更新答案。
为什么寻找最短的路呢?目的就是防止不断跳横叉边反悔卡住。在走最短路时,相同深度节点之间的路并没有起到向汇点流动的作用,可以先不用流。
注意 EK 算法中标号会不断变化。因此横叉边也不是不可能没有流量。
这个算法时间复杂度是多少呢?一次 bfs 会寻找到一条增广路,而 bfs 的时间复杂度显然是 $O(m)$,而增广总轮数上界是 $O(nm)$ 的,因此时间复杂度是 $O(nm^2)$。
Dinic 算法:竞赛不卡
竞赛网络流会卡 FF、EK,但是不卡 Dinic,因为 Dinic 的时间复杂度是 $O(n^2m)$。
Dinic 算法相较于 EK 算法做了一个改进就是一轮编号之后利用 dfs 进行多路增广。
但是这样会被一些数据 hack 掉,比如: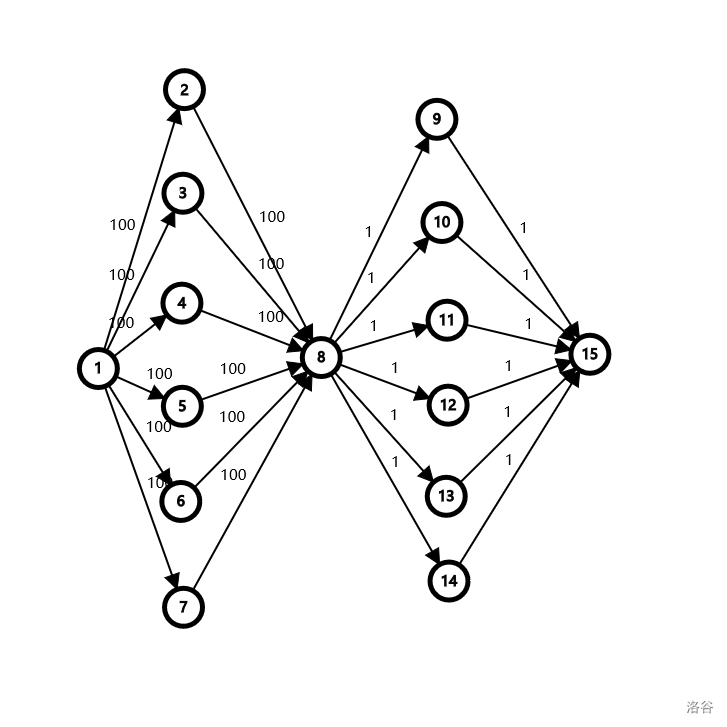
其中 $1$ 为源点而 $15$ 为汇点。现在第一股 $100$ 的流从 $2$ 流到 $8$,这些流可以轻松地填满 $8$ 到 $15$ 的所有弧。而当第二股流流过来时,它还需要便利所有被填满的弧,……这样会发现第一半的边每个边都要乘上第二段的所有边。当数据大的时候就很明显,这样还是 $O(nm^2)$ 的。
为了避免这样的情况,我们维护一个当前弧指针 $cur_i$,表示第一条还可能有剩余流量的弧(或者没有)。这样下一次流到这里时前面的弧都流满了,只需要从 $cur_i$ 开始继续就可以了。
优化后的时间复杂度就很优秀了,为 $O(n^2m)$。
最小割
定义一个割为将原图点集 $V$ 分为 $S,T$ 两个子集,使得 $s\in S,t\in T$ 的权值
之值。最小割就是使 $C$ 最小的割。
什么?最大流就等于最小割?证明
费用流
现在一个弧不仅有流量限制,还有单位花费,在弧 $i$ 上流 $1$ 单位流量的花费是 $c_i$。
做法也很简单,利用 EK 算法或者 Dinic 算法,只不过将 bfs 中深度改为从源点的最短路(边权是 $c_i$)。
常见模型
说实话模型才是网络流的核心
二分图匹配
我们考虑到一个左部点只能和一个右部点相匹配,可以看成一个左部点只能流出 $1$ 流量;同样一个右部点也只能接受 $1$ 流量。
因此我们建立超级源汇点 $s,t$,将 $s$ 向左部点连接容量 $1$,沿着 $m$ 条边从左部点向右部点连 $1$,再从右部点向 $t$ 连接 $1$。最后跑网络最大流即为答案。
事实上,Dinic 算法在二分图上的效率十分优秀,为 $O(n\sqrt n)$。
二选一
有 $n$ 个物品和两个集合 $A,B$。如果你将第 $i$ 个物品放入 $A$ 集合你会花费 $a_i$ 的代价;放入 $B$ 中会花费 $b_i$ 的代价,不能不放。同时还有 $m$ 条限制,每条限制形如 $(u_i,v_i,w_i)$,表示如果 $u_i,v_i$ 不在同一个集合就要花费额外的 $w_i$。求最小花费。
经典的最小割题目。我们建立超级源汇 $s,t$,对于一个点 $u$,我们连接边 $s\to u:a_u$ 和 $u\to v:b_u$,以及所有 $u\to v:w$。原图的最小割就是答案。因为我切掉 $s\to u$ 表示 $u$ 在 $A$ 集合,切掉 $u\to t$ 表示 $u$ 在 $B$ 集合,并且切掉 $u\to v$ 表示 $u,v$ 一定不在同一集合。就做完了。
最大权闭合子图
给定一张有向图,每个点都有一个权值(可以为正或负或 $0$ ),你需要选择一个权值和最大的子图,使得子图中每个点的后继都在子图中。
此题的建模十分巧妙,方法如下:
建立超级源汇 $s,t$。对于一个节点 $u$,若 $val_u$ 为正,则从 $s$ 向 $u$ 连接容量 $val_u$ 的弧;否则从 $u$ 向 $t$ 连接容量为 $-val_u$ 的弧。对于原图的每一条边 $(u,v)$,连接一条容量为 $\infty$ 的边。最后所有正权值的和减去此网络的最小割就是答案。这里割掉正点代表不选,割掉负点代表选择。
我们考虑一个图:
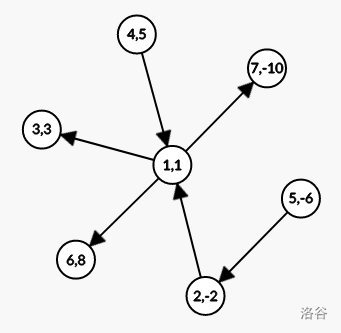
那么这个图的生成网络就是这样子的:
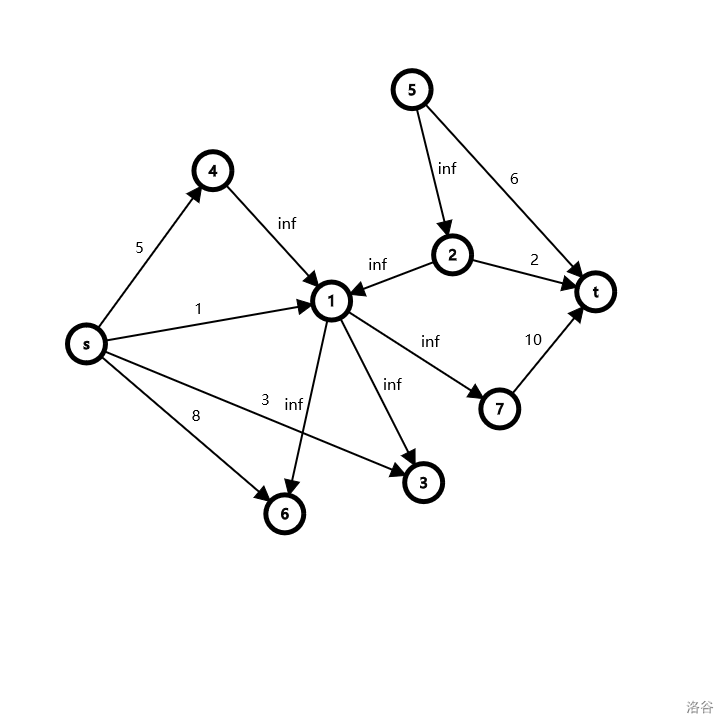
首先我们证明一下得到的答案是合法的,即这个构造是闭合子图:
显然不割掉一条源点流出的边就会让 $u$ 被选择,同时流量能够流到后继的点上。如果 $u\to v$ 并且 $v$ 是正权点,那么由于 $u\to v$ 权值是 $\infty$,所以一定联通,割掉 $s\to v$ 无意义,所以正权点 $u$ 后继的所有正权点都会被选择。同时为了保证 $s-t$ 不联通,需要割掉 $u$ 后继中的所有负权点,所以如果选择了一个正权点那么所有的后继负权点都会被选择。
其次我们来看这个是否为最优的:
注意到我们的最小割 $=$ 不被选择的正权点点权之和 $+$ 被选择的负权点权值绝对值之和,用所有正权点点权和减去,就是 被选择的正权点点权之和 $-$ 被选择的负权点权值绝对值之和,是正确的。由于这是最小割所以答案最大,满足要求。