树上问题

树的定义

图论定义：无向无环连通图。

等价定义：无相连通图，$n$ 个点和 $n-1$ 条边；$n$ 个点和 $n-1$ 条边的图，任意两个点之间有且仅有一条简单路径可以到达……

更具体的来说，树是一张无向图 $\mathcal T=(V,E)$，其中 $|E|=|V|-1$ 且任意两个点都联通。同时定义有根树和无根树的概念：有根树在 $V$ 中有一个特殊元素 $root$ 作为整棵树的根，而无根树没有。对于有根树，定义点 $u$ 的深度 $dep_u=\operatorname{dis}(u,root)$。

直径、半径等问题

直径的定义：树上长度最大的路径长度。

半径的定义：随意定节点为根时整棵树的深度最小值。

解决直径半径等问题的主要方法是树形 dp。

直径

树形 dp 求解

首先我们钦定 $1$ 为根。

我们考虑设 $f_u$ 表示从点 $u$ 向下走的最大深度。显然有

$$f_u=\max\{f_v+w(u,v)\}$$

我们再设 $g_u$ 为 $u$ 子树中直径长度。显然路径可以分成两种：穿过 $u$ 的和不穿过 $u$ 的。我们考虑求出所有 $u$ 儿子 $v$ 的 $f_v$ 第一第二大 $\mathrm{first},\mathrm{second}$，那么答案可以记作

$$g_u=\max(\max\{g_v\},f_\mathrm{first}+w(u,\mathrm{first})+f_\mathrm{second}+w(u,\mathrm{second}))$$

两次 dfs 求解

引理：对于一棵树上的点 $u$，距离 $u$ 最远的点一定是树上某条直径的端点之一。

证明 考虑反证法。设距离 $u$ 最远的点是 $v$。考虑一条直径 $(l,r)$，不妨设 $l$ 距离 $u$ 比 $r$ 更远。那么

$$\operatorname{dis}(u,v)>\operatorname{dis}(u,l)$$

因此

$$\begin{aligned} \operatorname{dis}(v,r)&=\operatorname{dis}(u,v)+\operatorname{dis}(u,r)\\ &>\operatorname{dis}(u,l)+\operatorname{dis}(u,r)=\operatorname{dis}(l,r) \end{aligned}$$

这与 $(l,r)$ 是直径矛盾。因此引理成立。

因此我们不妨钦定 $1$ 为根来对整棵树求出深度。因为深度就是点到根的距离，因此深度最大的点一定是直径端点之一。记这个点为 $u$，以它为根进行第二次 dfs 来求出深度，记深度最大的点为 $v$，那么 $(u,v)$ 一定是一条直径。（注意到直径不一定唯一）

半径

考虑换根 dp 求解。在上面 dp 求直径的 $f_u$ 基础上设 $h_u$ 为 $u$ 向上走的最长距离（可以去到兄弟）。

那么显然有 dp 方程

$$h_u=w(u,\mathrm{father})+\max(h_{\mathrm{father}},\max_{v\in\mathrm{brother}\ u}\{f_v+\operatorname{dis}(\mathrm{father},v)\})$$

那么以 $u$ 为根的时候树的深度就是 $f_u+h_u$，那么树的半径就是

$$\min\{f_u+h_u\}$$

例题：SDOI2024 第二轮省级 D6T3 粉兔的154

这是一道构造题。

给定一个数组 $a_1,a_2,\dots,a_n$，其中 $a_i=-1$ 或 $a_i\in[1,n]$，你需要构造一棵有 $n$ 个点的无根树，每条边权都为 $1$，满足对于点 $u$：

• 若 $a_u=-1$，则存在至少两个树上的点 $v_1,v_2$ 使得 $\operatorname{dis}(u,v_1)=\operatorname{dis}(u,v_2)>\operatorname{dis}(u,v)$，其中 $v\neq v_1$ 且 $v\neq v_2$。
• 否则一定满足 $\operatorname{dis}(u,a_u)>\operatorname{dis}(u,v)$，其中 $v\neq a_u$。

给出构造或者判定不可能。

$n\le10^6$。记 $S$ 为 $a_i$ 组成的集合，则分 subtask：

$n\le10$，$|S|=1\sim 4$，无限制。

子任务很神奇，先看子任务。

$n\le 10$

写个爆搜枚举父亲即可，时间复杂度 $O(n\times n!)$。

为啥要写暴力。因为暴力能完美规避大量 corner。

$|S|$ 的限制

以下默认 $n>10$。

当 $a_i$ 全部相同的时候，显然 $a_i=-1$ 有解，否则无解。$a_i=-1$ 的时候菊花图满足条件。

$|S|=2$ 时候，我们先不考虑 corner case。当 $-1\in S$ 的时候，通过玩我们可以找到这样一个符合条件的结构：

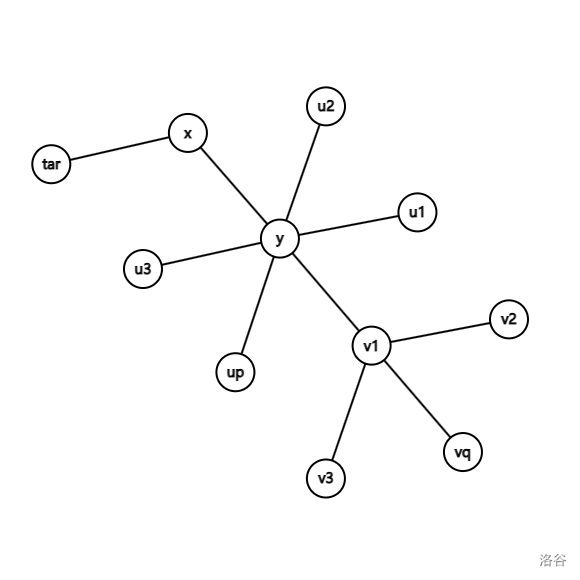
其中 $tar$ 是唯一非 $-1$ 的 $a_i$ 的值，$a_x=a_y=a_{u_1}=a_{u_2}=\dots=a_{u_p}=-1$，$a_{v_1}=a_{v_2}=\dots=a_{v_q}=tar$。

考虑这种情况下什么不行。容易发现 $q\le 2$ 不可以。

在继续讨论之前，我们先证明一个引理：$S$ 中有 $3$ 个非 $-1$ 元素时一定无解。

证明 不妨设 $S$ 中三个非 $-1$ 元素为 $v_1,v_2,v_3$。考虑到 $(v_1,v_2)$ 以及 $(v_1,v_3)$ 都是直径，考察一个 $a_u=v_2$ 的 $u$，显然 $\operatorname{dis}(u,v_2)=\operatorname{dis}(u,v_3)$（无论大于还是小于都会破坏假设），因此 $a_u$ 应当等于 $-1$。矛盾。

因此我们排除了很多情况。因此我们只剩下两种情况：$S=\{v_1,v_2\}$ 和 $S=\{v_1,v_2,-1\}$。

最后的讨论

这两种情况是本质相同的：$(v_1,v_2)$ 是树上的唯一直径。

考虑将 $a_u=v_1$ 的点挂在 $v_2$ 一侧，相反的挂在另一侧，$a_u=-1$ 的挂在中间，则最后会形成

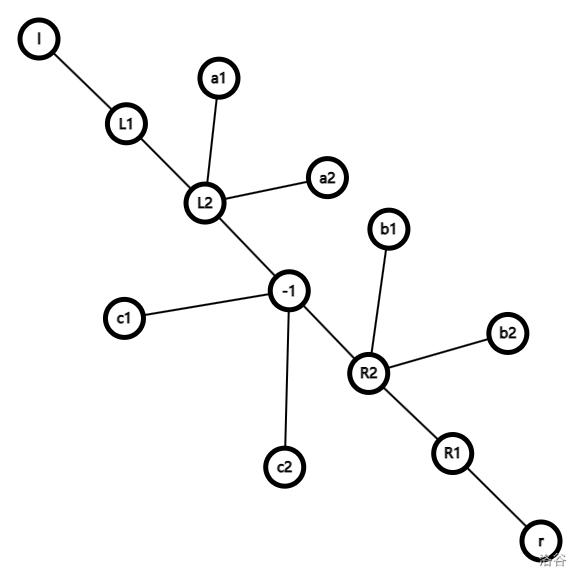
特殊情况就是（$s_l\le 2$ 或 $s_r\le 2$）且 $|s_l-s_r|\neq0$ 时无解。

小心 vector 爆炸导致 RE。

反过头来

大家可以仔细想想如果不打暴力会怎么样。

• $n=1$ 时需要特判若 $a_1\neq-1$ 无解否则有解。
• $n=2,3$ 时树结构确定，需要特判。
• ……

非常恶心。

最后

小粉兔有了另一段坚毅无私的黑历史。

虚树

见 虚树学习笔记。

LCA

定义啥的不说了。

例题：CF519E A and B and Lecture Rooms

给定一个 $n$ 个点的树，边权为 $1$，你需要回答 $q$ 次询问，每次询问给定 $u,v$，你需要统计满足条件的点 $p$ 的数量使得 $\operatorname{dis}(u,p)=\operatorname{dis}(v,p)$。

$n,q\le10^5$。

不妨钦定 $1$ 为根，我们需要找到 $(u,v)$ 路径上的中点，接在那个点上的所有点都满足条件。

怎么找点？首先求出 $\operatorname{dis}(u,v)$，再求出一半的长度。不妨令 $dep_u>dep_v$，那么从 $u$ 向上跳即可找到中点 $mid$。最后求出挂在上面的点数量就可以了（其实就是减掉旁边的分支）。注意特判 $u=v$。

时间复杂度 $O((n+q)\log n)$。